This is where navigation should be.


GSP_DEMO_GRAPH_TV - Reconstruction of missing sample on a graph using TV

Description

In this demo, we try to reconstruct missing sample of a piece-wise smooth signal on a graph. To do so, we will minimize the well-known TV norm defined on the graph.

For this example, you need the unlocbox. You can download it here: http://unlocbox.sourceforge.net/download

We express the recovery problem as a convex optimization problem of the following form:

\begin{equation*} arg \min_x \|\nabla(x)\|_1 \text{ s. t. } Mx = y \end{equation*}

Where b represents the known measurements, M is an operator representing the mask and \(\epsilon\) is the radius of the l2 ball.

We set

  • \(f_1(x)=||\nabla x ||_1\) We define the prox of \(f_1\) as:

    \begin{equation*} prox_{f1,\gamma} (z) = arg \min_{x} \frac{1}{2} \|x-z\|_2^2 + \gamma \| \nabla z \|_1 \end{equation*}

  • \(f_2\) is the indicator function of the set S define by \(Mx = y\) We define the prox of \(f_2\) as

    \begin{equation*} prox_{f2,\gamma} (z) = arg \min_{x} \frac{1}{2} \|x-z\|_2^2 + i_S(x) , \end{equation*}

    with \(i_S(x)\) is zero if x is in the set S and infinity otherwise. This previous problem has an identical solution as:

    \begin{equation*} arg \min_{x} \|x - z\|_2^2 \hspace{1cm} such \hspace{0.25cm} that \hspace{1cm} Mx = y \end{equation*}

    It is simply a projection on the B2-ball.

Results

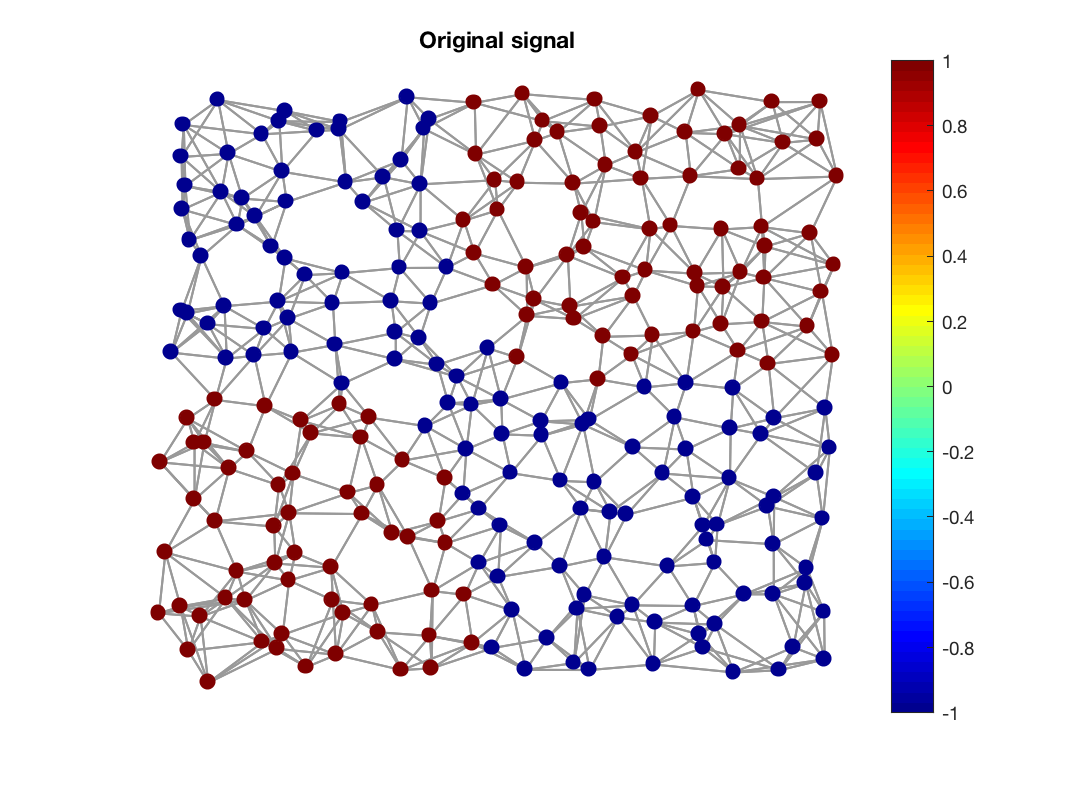
gsp_demo_graph_tv_1.png

Original signal on graph

This figure shows the original signal on graph.
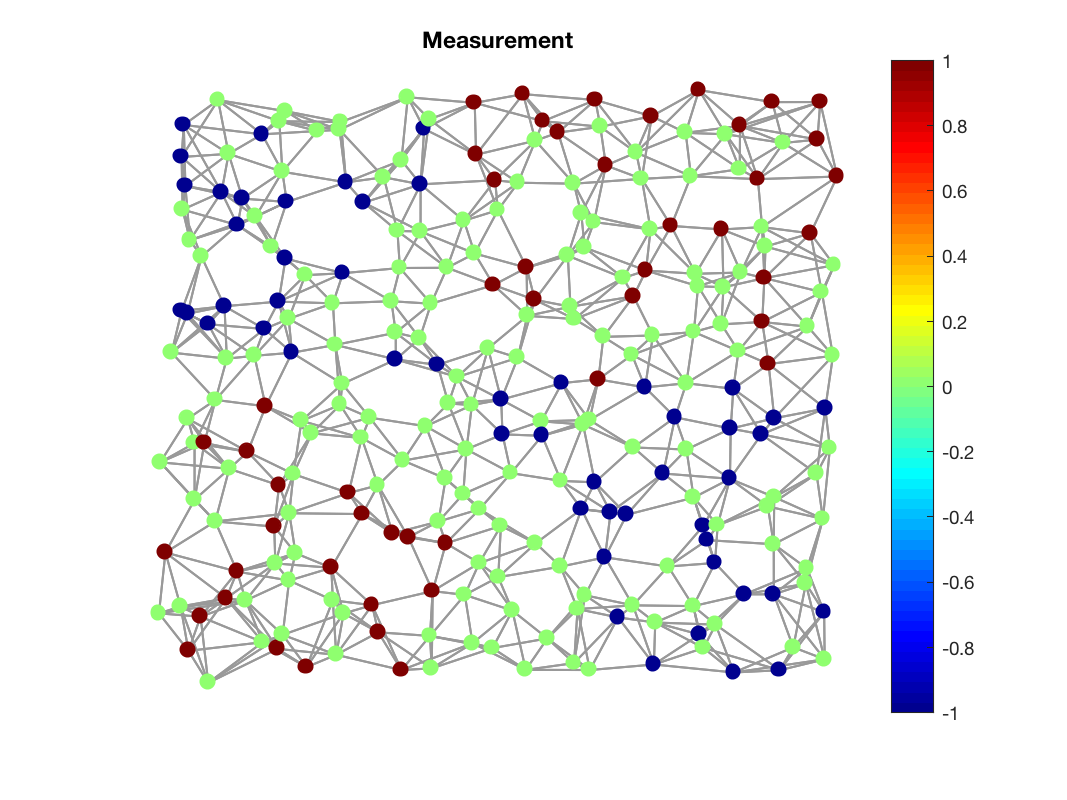
gsp_demo_graph_tv_2.png

Depleted signal on graph

This figure shows the signal on graph after the application of the mask and addition of noise. Half of the vertices are set to 0.
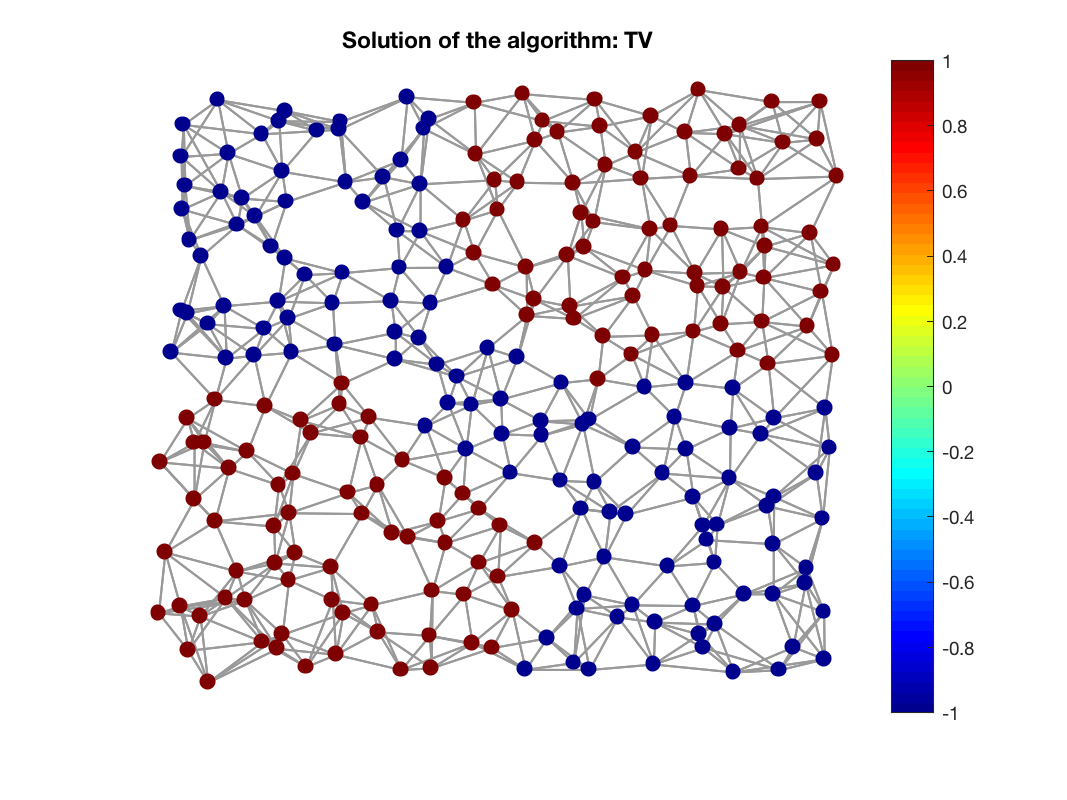
gsp_demo_graph_tv_3.png

Reconstructed signal on graph usign TV

This figure shows the reconstructed signal thanks to the algorithm.

Comparison with Tikhonov regularization

We can also use the Tikhonov regularizer that will promote smoothness. In this case, we solve:

\begin{equation*} arg \min_x \tau \|\nabla(x)\|_2^2 \text{ s. t. } \|Mx-b\|_2 \leq \epsilon \end{equation*}

The result is presented in the following figure:

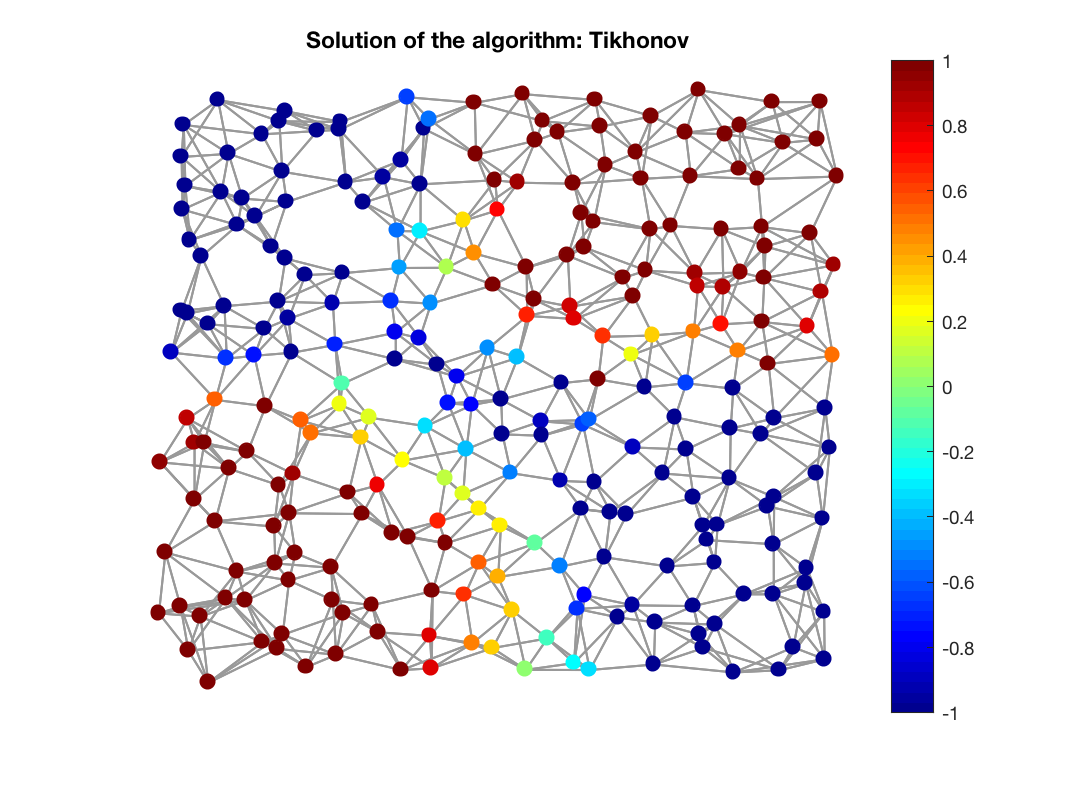
gsp_demo_graph_tv_4.png

Reconstructed signal on graph using Tikhonov

This figure shows the reconstructed signal thanks to the algorithm.

This code produces the following output:

UnLocBoX version 1.7.3. Copyright 2012-2015 LTS2-EPFL, by Nathanael Perraudin
CHAMBOLLE_POCK   Rel primal: 1.755268e-04, rel dual 3.066232e-04, it = 200, MAX_IT
Using direct solution