GSP_DEMO_PYRAMID - Demonstration of the use of the graph pyramid
Description
In this demonstration file, we show how to reduce a graph using the GSPBox. Then we apply the pyramid to a simple signal.
The function gsp_graph_multiresolution computes the graph pyramid for you:
param.sparsify = 1; Gs = gsp_graph_multiresolution(G, Nlevel,param);
Gs is a cell array of graph representing the pyramid of graphs. Here all optional parameter are important:
- param.sparsify: When a graph is reduced, the density of edges has tendency to be amplified. One way to counterbalance this effect is to sparsify the graph for each sublevel. The function gsp_graph_sparsify is used to perform this operation. However, this could lead to bad graphs (disconnected for instance).
- sparsify_epsilon: Parameter epsilon used in the sparsification
- param.filters: is a cell array of filters (or a single filter). Thoses filter will be used in the analysis and synthesis operator.
Let's display the results:
figure;
for ii = 1:numel(Gs)
subplot(2,3,ii)
gsp_plot_graph(Gs{ii})
title(['Reduction level: ', num2str(ii-1)]);
end
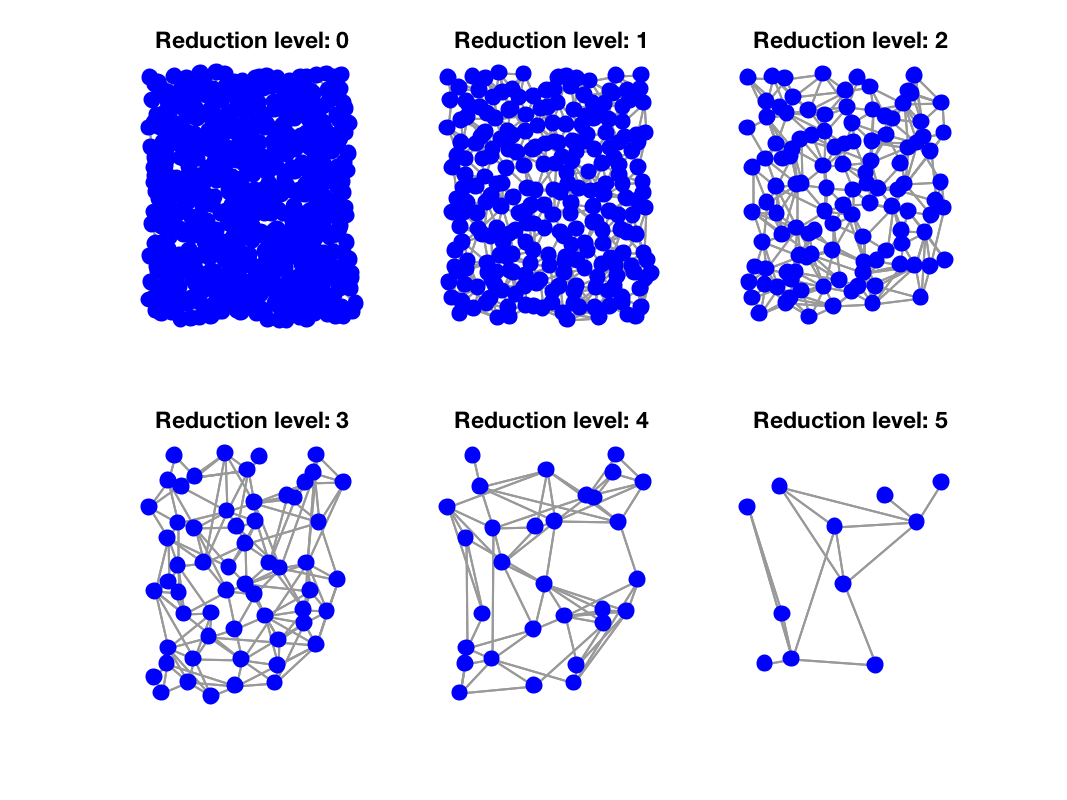
Reduction of the graph
Now that we have precomputed the pyramid of graphs, we can apply it to a signal. Here we create a signal that is smooth over the graph but with a big discontinuity in the middle

Signal to be analysed
The graph pyramid can be simply applied thanks to the function gsp_pyramid_analysis:
[ca,pe]=gsp_pyramid_analysis(Gs,f);
ca contains the coarse approximation of each level and pe the prediction errors. Let's display them:
figure
paramplot.show_edges = 0;
for ii = 1:numel(Gs)
subplot(2,3,ii)
gsp_plot_signal(Gs{ii},pe{ii},paramplot);
title(['P. E. level: ', num2str(ii-1)]);
end
figure
for ii = 1:numel(Gs)
subplot(2,3,ii)
gsp_plot_signal(Gs{ii},ca{ii},paramplot)
title(['C. A. level: ', num2str(ii-1)]);
end
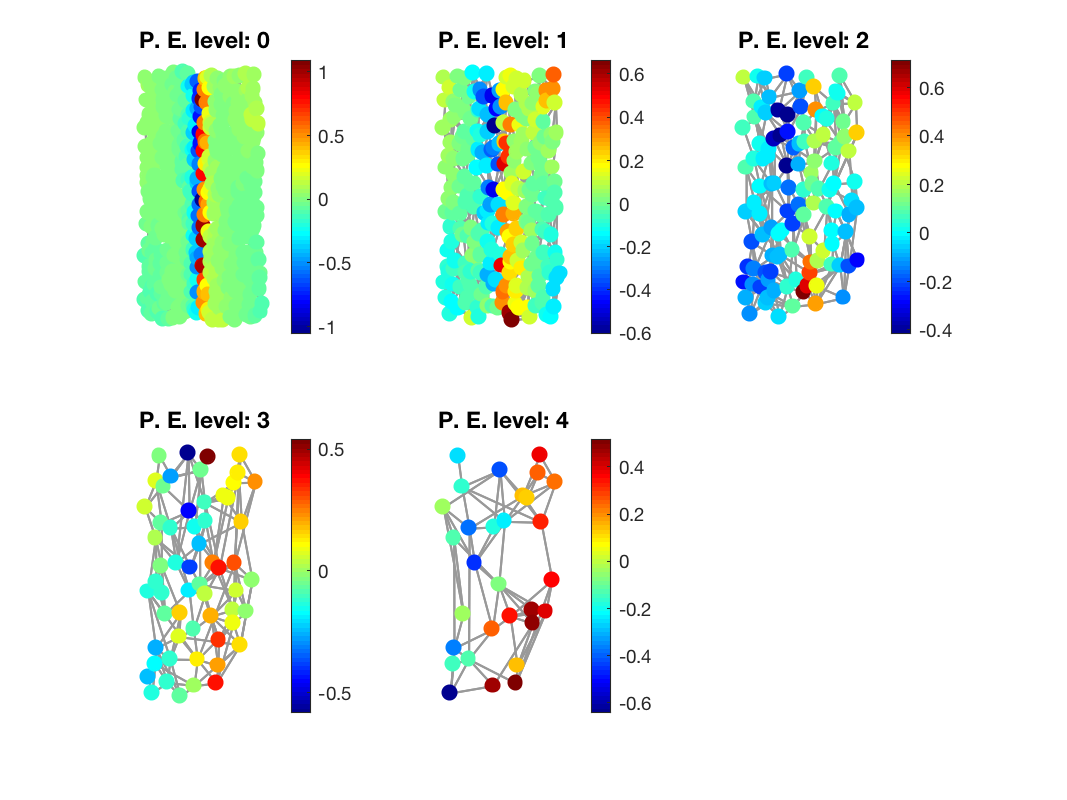
Prediction errors
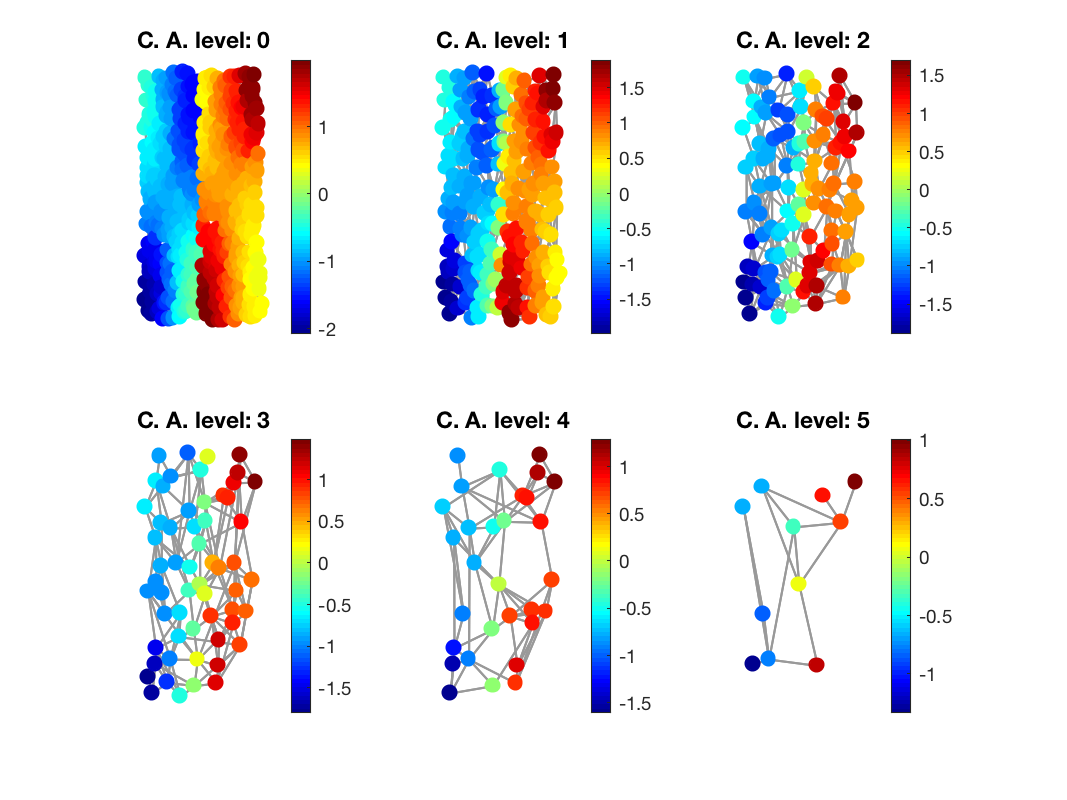
Coarse approximations
Finally, you can perform a synthesis operation using the function gsp_pyramid_synthesis
coeff = gsp_pyramid_cell2coeff(ca,pe); f_pred = gsp_pyramid_synthesis(Gs,coeff);
The function gsp_pyramid_cell2coeff remove all unecessary coefficients and keep only the last sublevel and the prediction error.
Enjoy!
This code produces the following output:
The relative reconstruction error is : 1.64455e-15