GSP_DEMO_STATIONARITY - Demonstration to use stationarity
Description
This demonstration uses the theory developed in the paper "Stationary graph signal processing?, Nathanael Perraudin and Pierre Vandergheynst, arXiv:1601.02522, http://arxiv.org/pdf/1601.02522
We use Wiener optimization to solve an in-painting problem. We suppose that the Power Spectral Density (PSD) of the input signal is unknown and we estimate it using a single signal. The PSD is estimated using the function gsp_estimate_psd
parampsd.Nfilt = 100; psd_est = gsp_estimate_psd(G,X1,parampsd);
The parameter param.Nfilt selects the number of windows to use for the PSD estimation. A large number leads to a finer approximation. However it 1) increases the computation time for the estimation 2) necessitates a larger order of Chebyshev polynomial if exact filtering is not used. the Chebyshev order can be changed with:
parampsd.order = 50;
Once the PSD is computed, one can estimate a signal with the function gsp_wiener_inpainting
S = gsp_wiener_inpainting(G, Y, Mask, psd_est, sigma^2,param);
This function solves the Wiener optimization problem thanks to the UNLocBoX. You might want to change the precision of the recovery. To do so, you can set the parameter maxit and tol of the structure param:
param.maxit = 1000; % Maximum number of iterations param.tol = 1e-8; % Tolerance to stop iterating
Figures 1,2 and 3 show an inpainting example. Figure 4 shows the estimation of the PSD from only one measurement.
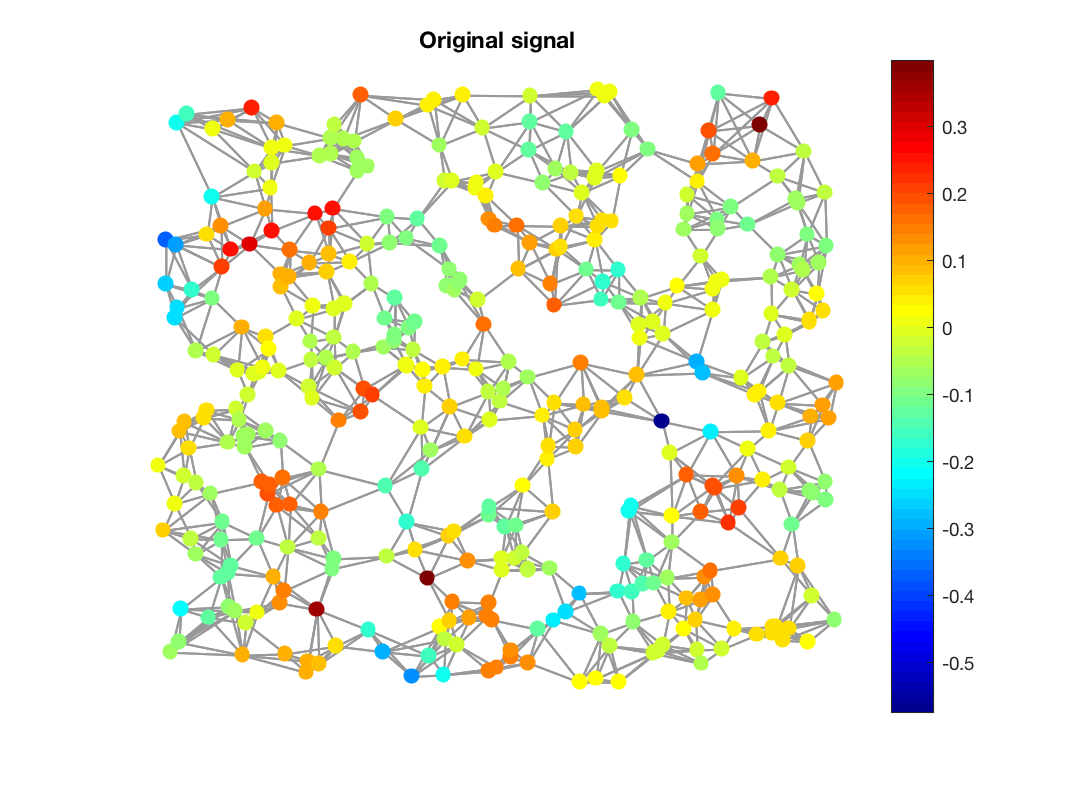
We generate a stationary signal
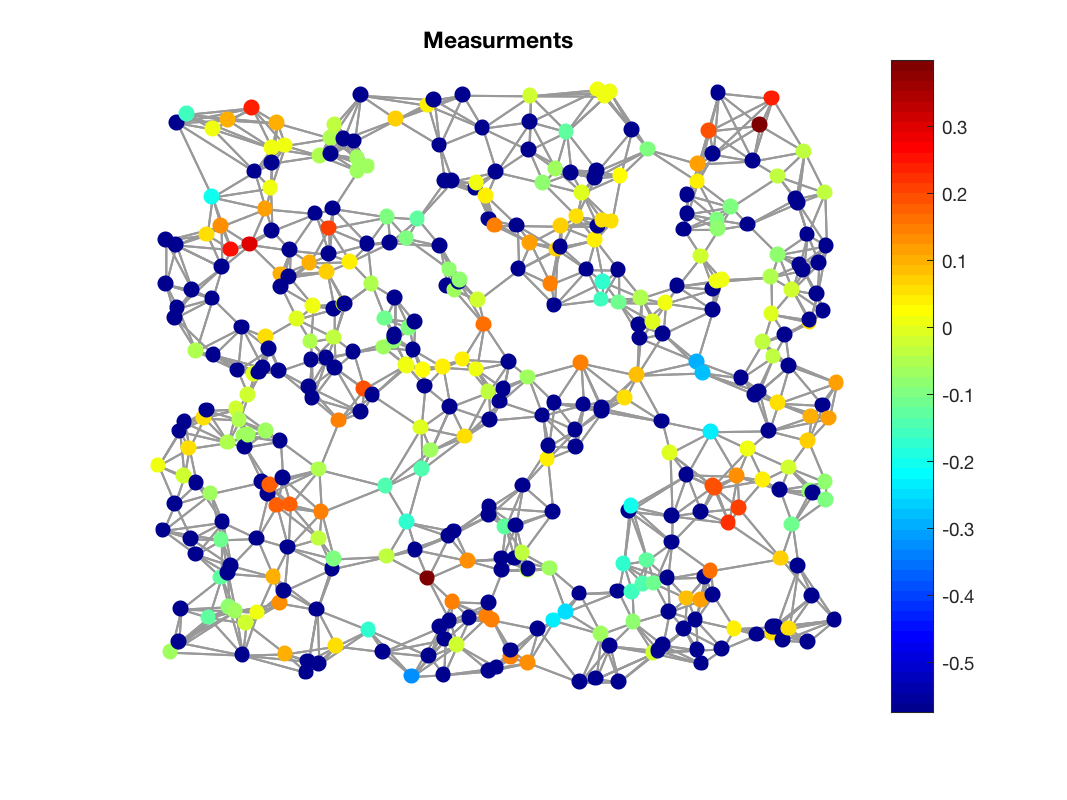
We randomly select 50% of the signal
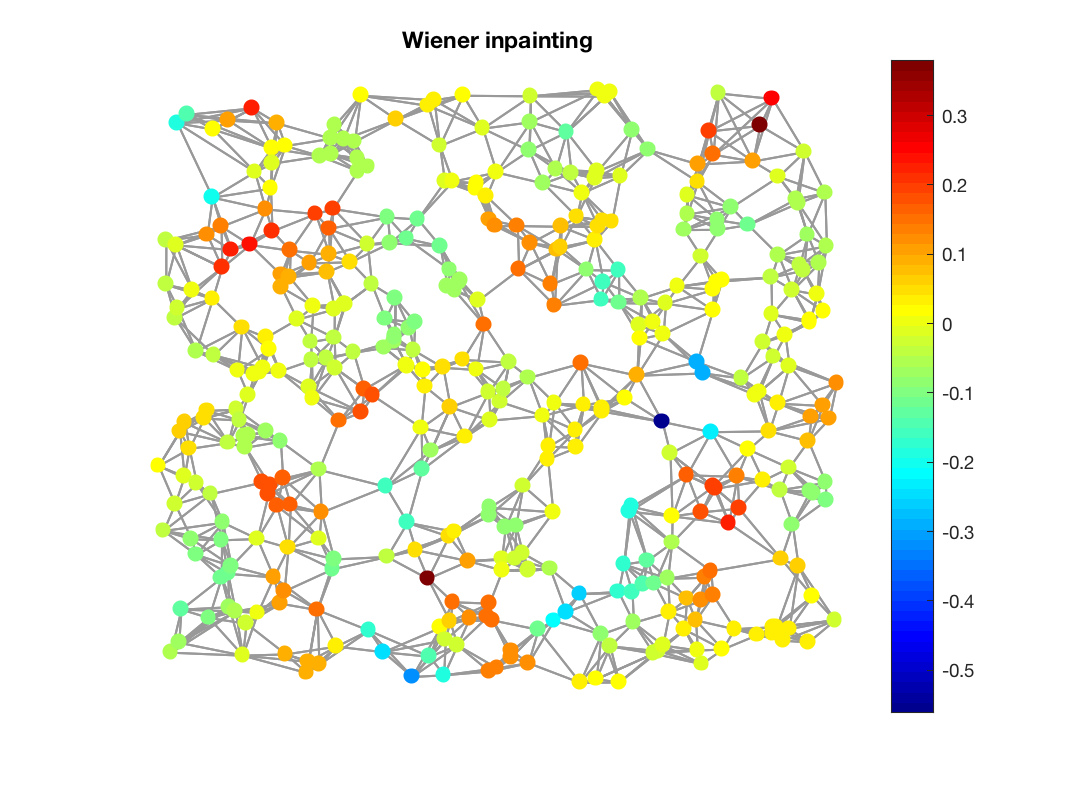
We reconstruction the signal using Wiener optimization
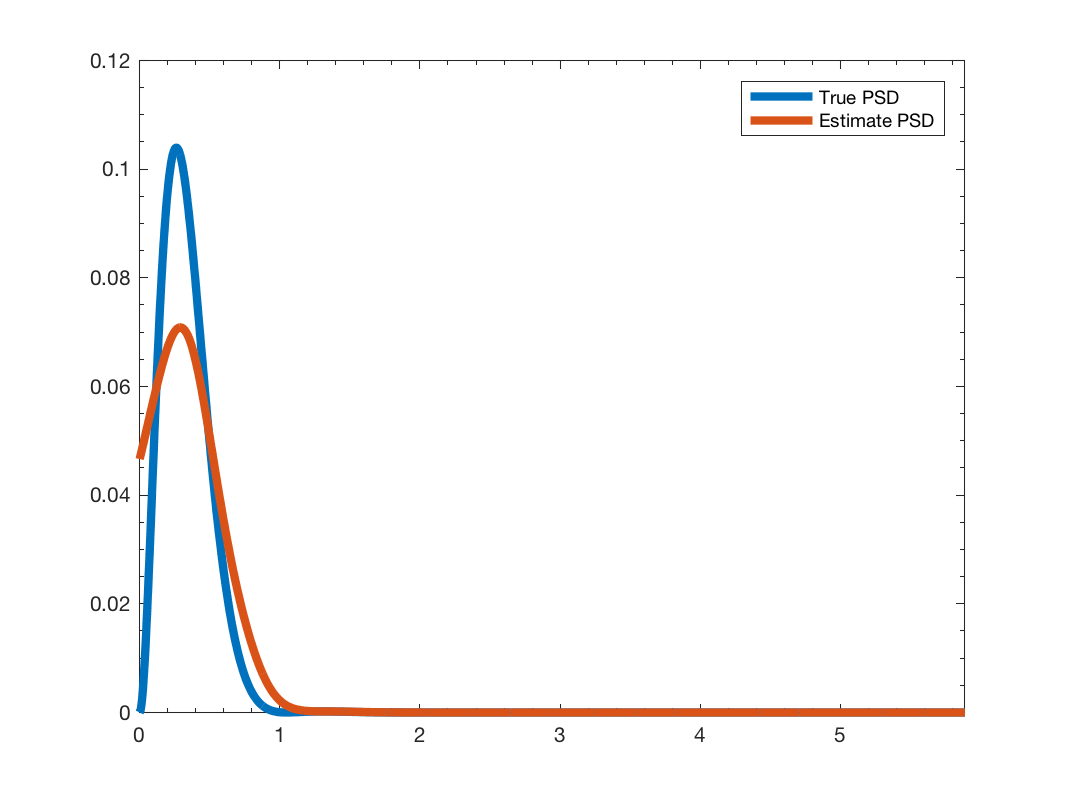
True VS approximated PSD
This code produces the following output:
DOUGLAS_RACHFORD f(x^*) = 1.290451e+03, rel_eval = 2.660961e-03, it = 200, MAX_IT
References:
N. Perraudin and P. Vandergheynst. Stationary signal processing on graphs. arXiv preprint arXiv:1601.02522, 2016.