This is where navigation should be.
GSP_DESIGN_EXPWIN - create an expwin window of lenth N with parameter a
Usage
g = gsp_design_expwin(G); g = gsp_design_expwin(G, bmax); g = gsp_design_expwin(G, bmax, a);
Input parameters
| G | Graph structure |
| bmax | Maximum relative band (default 0.2) |
| a | Slope parameter (default 1). |
Output parameters
| g | filter |
Description
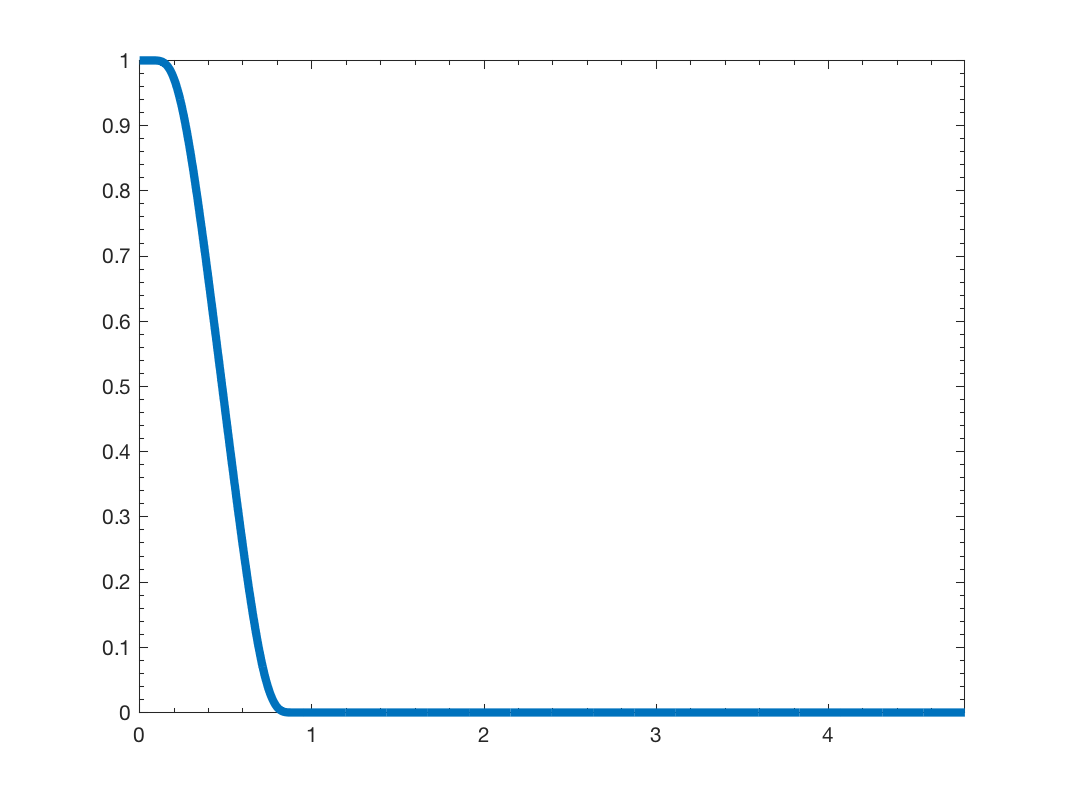
This function design the following filter:
\begin{equation*}
g(x) = s\left(\frac{1-x}{\lambda_{\text{max}} b_{\text{max}} }\right)
\end{equation*}
where \(s(x)\) is the step function
\begin{equation*}
s(x)=\begin{cases} 0 & \mbox{if }x<-1 \\\\ \frac{e^{-\frac{a}{x}}}{e^{-\frac{a}{x}}+e^{-\frac{a}{1-x}}} & \mbox{if }x\in[-1,1]\\\\ 1 & \mbox{if }x>1 \end{cases}
\end{equation*}
It uses a clever exponential construction to obtain an infinitely differentiable function that is band limited!
This function will compute the maximum eigenvalue of the laplacian. To be more efficient, you can precompute it using:
G = gsp_estimate_lmax(G);
Example:
Nf = 4; G = gsp_sensor(100); G = gsp_estimate_lmax(G); g = gsp_design_expwin(G); gsp_plot_filter(G,g);