This is where navigation should be.
GSP_DESIGN_REGULAR - Create a regular filterbank
Usage
g = gsp_design_regular( G ); g = gsp_design_regular( G, param );
Description
- Inputs parameters:
- G : Graph structure or lmax param : Structure of optional parameters
- Outputs parameters:
- g : filterbank
This function creates a parseval filterbank of \(2\) filters. The low-pass filter is defined by a function \(f_l(x)\) between \(0\) and \(2\). For \(d = 0\).
\begin{equation*}
f_{l}= \sin\left( \frac{\pi}{4} x \right)
\end{equation*}
For \(d = 1\)
\begin{equation*}
f_{l}= \sin\left( \frac{\pi}{4} \left( 1+ \sin\left(\frac{\pi}{2}(x-1)\right) \right) \right)
\end{equation*}
For \(d = 2\)
\begin{equation*}
f_{l}= \sin\left( \frac{\pi}{4} \left( 1+ \sin\left(\frac{\pi}{2} \sin\left(\frac{\pi}{2}(x-1)\right)\right) \right) \right)
\end{equation*}
And so on for the other degrees \(d\).
The high pass filter is adapted to obtain a tight frame.
This function will compute the maximum eigenvalue of the laplacian. To be more efficient, you can precompute it using:
G = gsp_estimate_lmax(G);
Example:
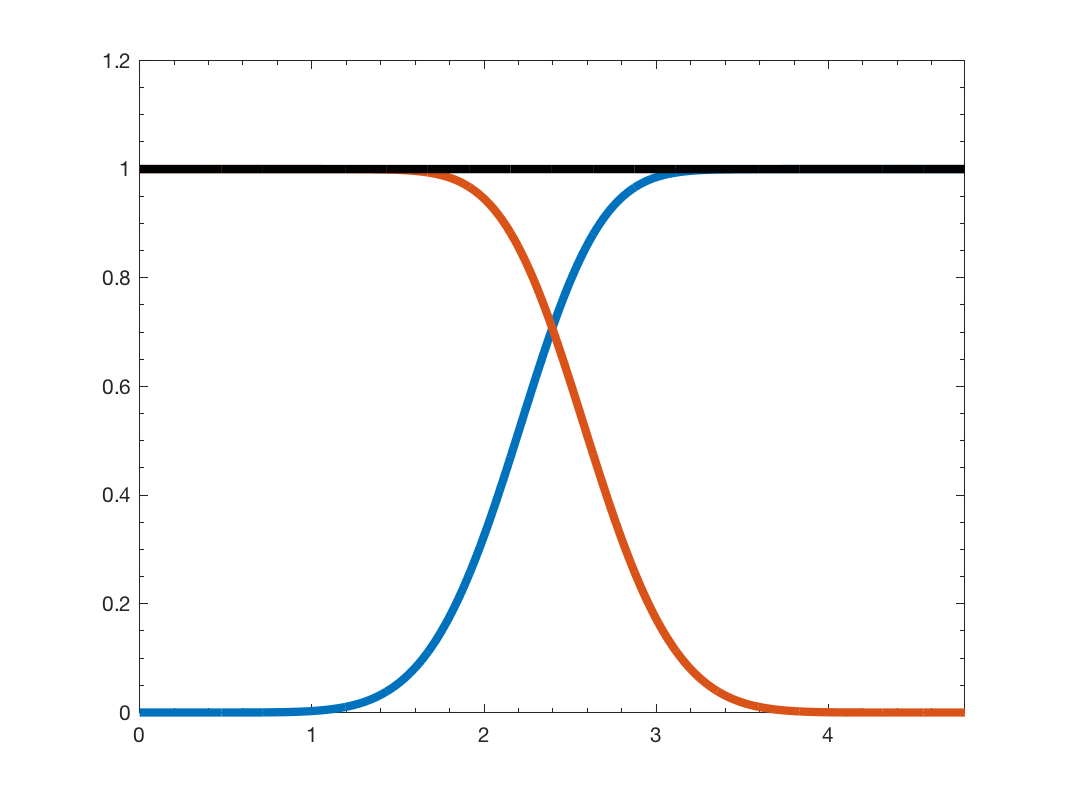
G = gsp_sensor(100); G = gsp_estimate_lmax(G); g = gsp_design_regular(G); gsp_plot_filter(G,g); [A,B] = gsp_filterbank_bounds(G,g)
This code produces the following output:
A =
1.0000
B =
1.0000
param is an optional structure containing the following fields
- param.verbose: verbosity level. 0 no log - 1 display warnings. (default 1)
- param.d: Degree. See equation for mor informations. (default 3)