This is where navigation should be.
GSP_FILTER_SYNTHESIS - Synthesis operator of a gsp filterbank
Usage
s = gsp_filter_synthesis(G, filters, c); s = gsp_filter_synthesis(G, filters, c, param);
Input parameters
| G | Graph structure. |
| filters | Set of spectral graph filters. |
| c | Transform coefficients |
| param | Optional parameter |
Output parameters
| signal | sythesis signal |
Description
'gsp_filter_synthesis(G,filters,c)' computes the synthesis operator for coefficient \(c\), where the atoms of the transform dictionary are generalized translations of each graph spectral filter to each vertex on the graph.
\begin{equation*}
f = D c
\end{equation*}
where the columns of \(D\) are \(g_{i,m}=T_i g_m\), and \(T_i\) is a generalized translation operator applied to each filter \(\hat{g}_m(\cdot)\).
Each column of c is the response of the signal to one filter.
Example:
Nf = 4; G = gsp_sensor(30); G = gsp_estimate_lmax(G); G = gsp_estimate_lmax(G); g = gsp_design_mexican_hat(G, Nf); f = zeros(G.N,1); f(1) = 1; f = G.L^2*f; ff = gsp_filter_analysis(G,g,f); f2 = gsp_filter_synthesis(G,g,ff); paramplot.show_edges = 1; figure() subplot(211) gsp_plot_filter(G,g) subplot(223) gsp_plot_signal(G,f,paramplot); subplot(224) gsp_plot_signal(G,f2,paramplot);
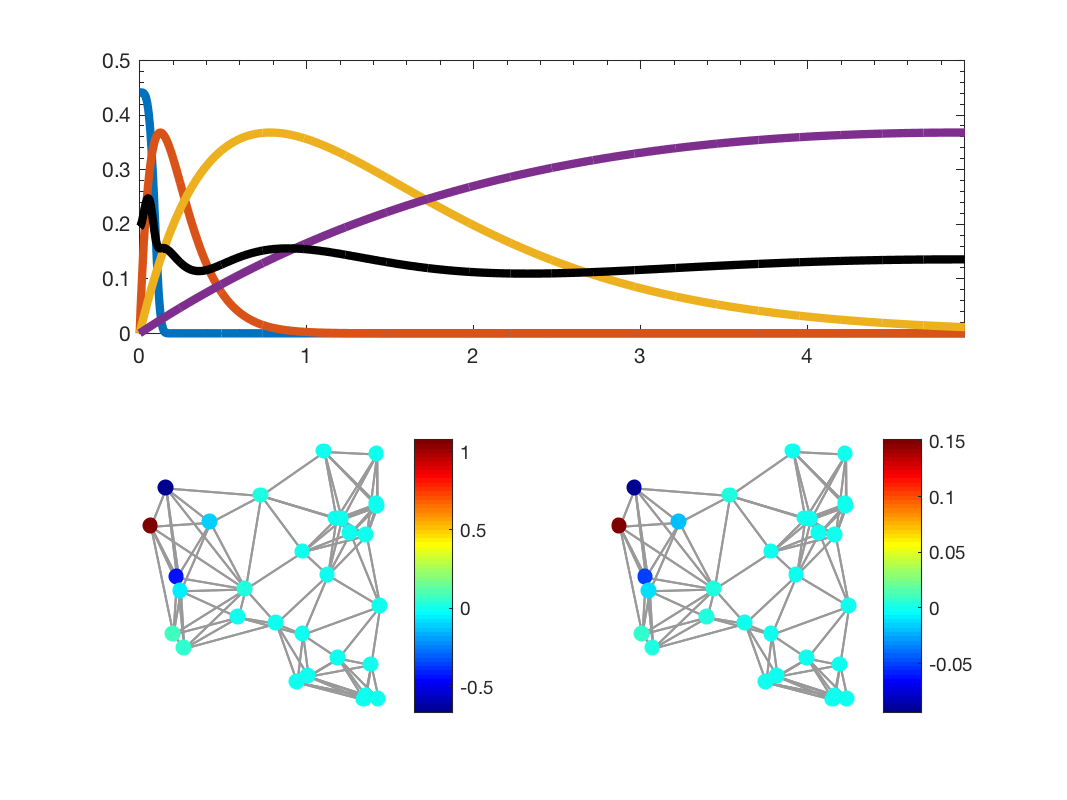
Additional parameters
- param.method : Select the method to be used for the computation. * 'exact' : Exact method using the graph Fourier matrix * 'cheby' : Chebyshev polynomial approximation * 'lanczos' : Lanczos approximation Default: if the Fourier matrix is present: 'exact' otherwise 'cheby'
- param.order : Degree of the Chebyshev approximation (default=30).
- param.verbose : Verbosity level (0 no log - 1 display warnings) (default 1).
References:
D. K. Hammond, P. Vandergheynst, and R. Gribonval. Wavelets on graphs via spectral graph theory. Appl. Comput. Harmon. Anal., 30(2):129--150, Mar. 2011.