RR_SPECTRO_MULT - Phase recovery problem for modified spectrograms

Description

Reproducible research addendum for phase recovery problem

AN EXTENDED GRIFFIN LIM ALGORTITHM

Paper: Perraudin Nathanael, Balazs Peter

Demonstration matlab file: Perraudin Nathanael

ARI -- April 2013

Dependencies

In order to use this matlab file you need the LTFAT toolbox. You can download it on http://ltfat.sourceforge.net

The problem

From a spectrogram S, we would like to recover the signal with the closest spectrogram.

The problem could be written in the form:

with

• \(S\) : The original spectrogram
• \(G\) : A frame
• \(x\) : The signal we would like to recover

Note that for these simulations, there is usually no x such that \(|Gx|=S\) because S are spectrogram modified coefficients.

Algorithms for solving the problem

We will compare 2 different algorithms to solve the problem

• Griffin-Lim : Original algorithm designed by griffin and Lim
• Forward-PBL : A modification of the Griffin-Lim

Goal of these simulations

Test the robustenes of the Forward-PBL algorithm for reconstruction signals from modified spectrogram.

We use a random spectrogram multiplier. The initial phase is the phase of the initial short time Fourier transform.

Results

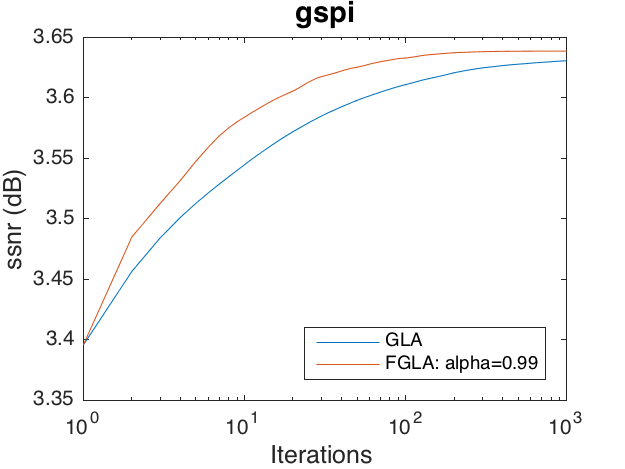
Phase recovery problem on 'gspi'

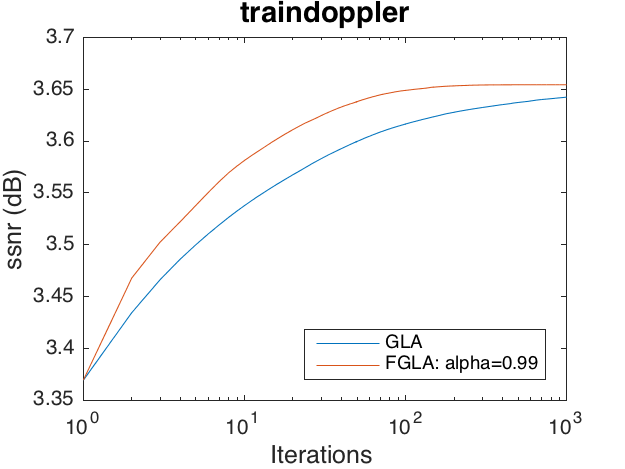
Phase recovery problem on 'traindoppler'

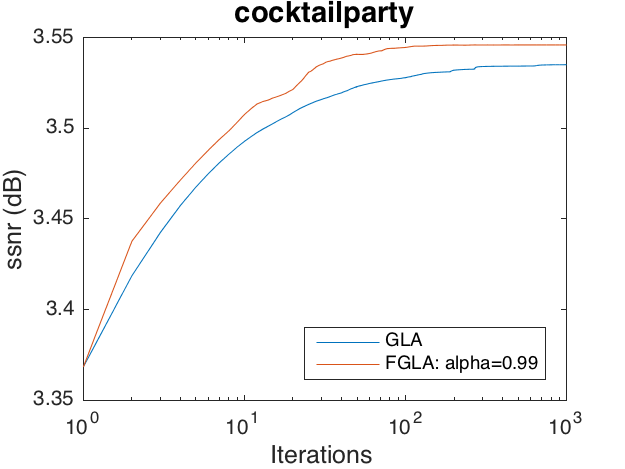
Phase recovery problem on 'cocktailparty'

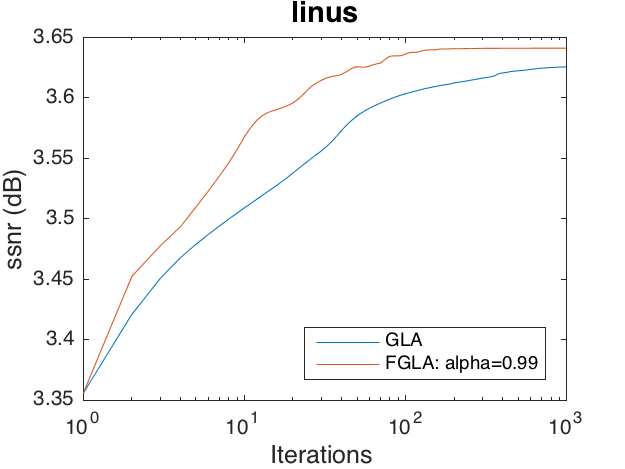
Phase recovery problem on 'linus'

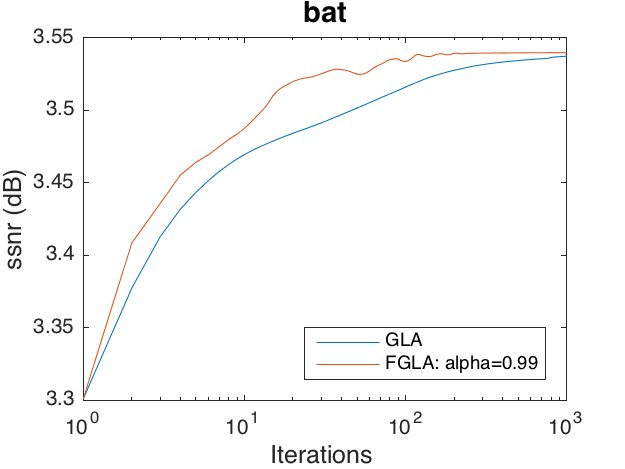
Phase recovery problem on 'bat'

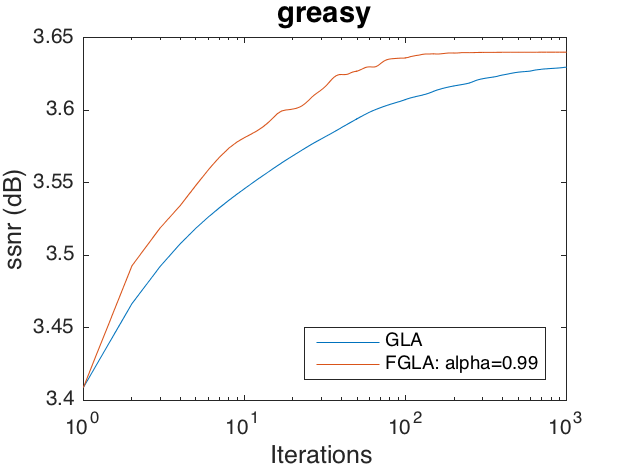
Phase recovery problem on 'greasy'

This code produces the following output:

LTFAT version 2.1.1. Copyright 2005-2015 Peter L. Søndergaard. For help, please type "ltfathelp". LTFAT is using the MEX backend.
(Your global and persistent variables have just been cleared. Sorry.)
-- Create the windows and the operators...  Done
-- Create the spectrogram muliplier...  Done
-- Reconstruction method:GLA
   * The obtained ssnr is: 3.63076
-- Reconstruction done
-- Reconstruction method:FGLA  with alpha = 0.99
   * Selected method: fast Griffin-Lim algorithm
   * The obtained ssnr is: 3.63877
-- Reconstruction done
-- Display the results...  Done
-- Create the windows and the operators...  Done
-- Create the spectrogram muliplier...  Done
-- Reconstruction method:GLA
   * The obtained ssnr is: 3.64252
-- Reconstruction done
-- Reconstruction method:FGLA  with alpha = 0.99
   * Selected method: fast Griffin-Lim algorithm
   * The obtained ssnr is: 3.65444
-- Reconstruction done
-- Display the results...  Done
-- Create the windows and the operators...  Done
-- Create the spectrogram muliplier...  Done
-- Reconstruction method:GLA
   * The obtained ssnr is: 3.53502
-- Reconstruction done
-- Reconstruction method:FGLA  with alpha = 0.99
   * Selected method: fast Griffin-Lim algorithm
   * The obtained ssnr is: 3.54591
-- Reconstruction done
-- Display the results...  Done
-- Create the windows and the operators...  Done
-- Create the spectrogram muliplier...  Done
-- Reconstruction method:GLA
   * The obtained ssnr is: 3.62572
-- Reconstruction done
-- Reconstruction method:FGLA  with alpha = 0.99
   * Selected method: fast Griffin-Lim algorithm
   * The obtained ssnr is: 3.64119
-- Reconstruction done
-- Display the results...  Done
-- Create the windows and the operators...  Done
-- Create the spectrogram muliplier...  Done
-- Reconstruction method:GLA
   * The obtained ssnr is: 3.53712
-- Reconstruction done
-- Reconstruction method:FGLA  with alpha = 0.99
   * Selected method: fast Griffin-Lim algorithm
   * The obtained ssnr is: 3.53957
-- Reconstruction done
-- Display the results...  Done
-- Create the windows and the operators...  Done
-- Create the spectrogram muliplier...  Done
-- Reconstruction method:GLA
   * The obtained ssnr is: 3.62956
-- Reconstruction done
-- Reconstruction method:FGLA  with alpha = 0.99
   * Selected method: fast Griffin-Lim algorithm
   * The obtained ssnr is: 3.63989
-- Reconstruction done
-- Display the results...  Done