Download r2π archive for windows or for unix


RR_SUPERRESOLUTION_FOR_SPECTROMETRY - Superresolution used in spectrometry

Description

Demonstration file on synthetic dataset

Author: Perraudin Nathanael

EPFL - LTS2 -- Mai 2014

Dependencies

In order to use this matlab file you need the UNLocbox toolbox. You can download it on https://lts2research.epfl.ch/unlocbox .

The problem

In this file, we attempt to increase the resolution of a signal in the Fourier domain. This signal is particular because we know that it is sparse. The original signal in the spectral domain is displayed in the figure 1.

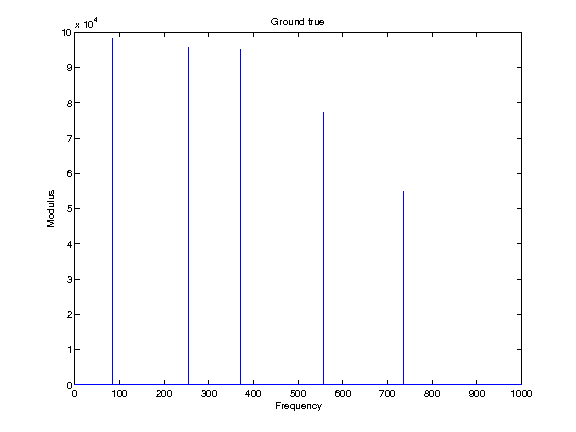
rr_superresolution_for_spectrometry_1.png

Fig 1: Original signal in the spectral domain

We consider this signal as the ground true for our problem.

This last signal pocess a very high resolution frequency resolution. To obtain such a frequency resolution, a very long time measurement is done. Let's suppose now, that we would like to reduce this measurment time to something shorter. This is equivalent to convolute the signal in the Fourier domain by a sinc. Figure 2 show the effect of this convolution. This operation is considered as masking of all unmeasured coefficients.

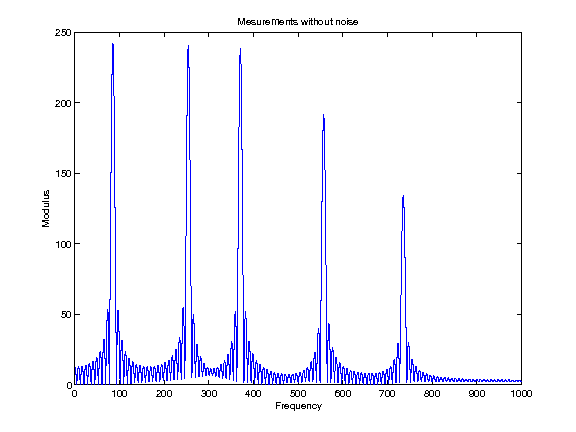
rr_superresolution_for_spectrometry_2.png

Fig 2: Blured signal

This signal is the result of the convolution with a sinc

Finally, we add some gaussian noise to test if our method is robust. Figure 3 display the noiy measurments that we use for our problem.

rr_superresolution_for_spectrometry_3.png

Fig 3: Noisy blured signal

Measurement used for our problem

To get close to the ground true, we will solve the following convex optimization problem:

\begin{equation*} \operatorname{argmin}_x \|F x\|_1 \text{ s. t. } \|M x - y \|_2 \leq \epsilon \end{equation*}

where \(y\) are the measurements, \(F^{-1}\) the inverse Fourier transform and \(M\) the masking operator. \(\epsilon\) is the radius of the \(l_2\)-ball that is chosen with respect of the noise.

Solving the problem lead to the following denoised signal.

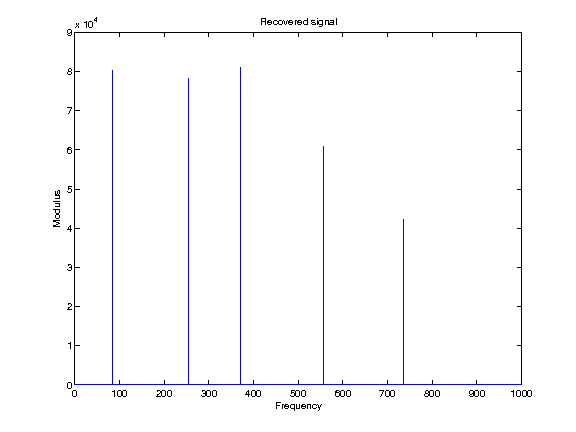
rr_superresolution_for_spectrometry_4.png

Fig 4: Denoised signal

Solution of the convex optimization problem

The problem is solved in two times. We compute a first estimate by solving the convex problem. Then with this rougth estimate, we guess the position and the amplitude of the dirac to obtain a new estimation. This estimation is then reinsterted as starting point into the convex problem to obtain a final solution.

This code produces the following output:

UnLocBoX version 1.3.135. Copyright 2012-2013 LTS2-EPFL, by Nathanael Perraudin
  Solution found: ||f|| = 3.807219e+05, rel_norm = 9.886311e-10, REL_NORM
  Solution found: ||f|| = 3.802400e+05, rel_norm = 5.448702e-10, REL_NORM