SYNTHETIC_WIENER_DECONVOLUTION - Wiener deconvolution experiment on a synthetic dataset

Description

Authors: Nathanael Perraudin and Pierre Vandergheynst

Date: January 2016

Paper: Stationary signal processing on graphs

Abstract of the paper

Graphs are a central tool in machine learning and information processing as they allow to conveniently capture the structure of complex datasets. In this context, it is of high importance to develop flexible models of signals defined over graphs or networks. In this paper, we generalize the traditional concept of wide sense stationarity to signals defined over the vertices of arbitrary weighted undirected graphs. We show that stationarity is intimately linked to statistical invariance under a localization operator reminiscent of translation. We prove that stationary signals are characterized by a well-defined Power Spectral Density that can be efficiently estimated even for large graphs. We leverage this new concept to derive Wiener-type estimation procedures of noisy and partially observed signals and illustrate the performance of this new model for denoising and regression.

This experiment

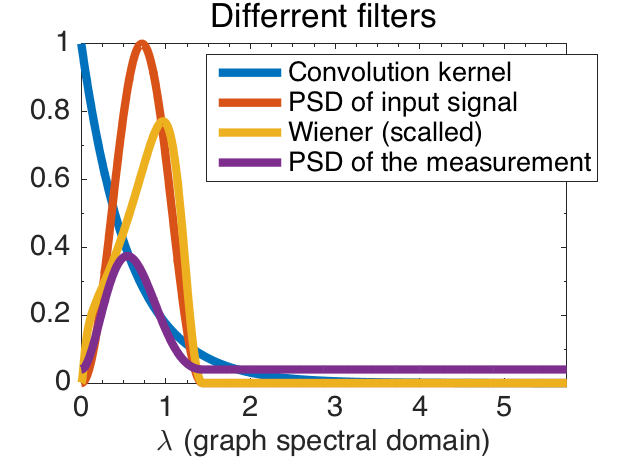
We start with a de-convolution example on a random geometric graph. This can model an array of sensors distributed in space or simply a mesh. The signal is chosen with a low frequency band-limited PSD. To produce the measurements, the signal is convolved with the heat kernel \(e^{-\tau x}\). Additionally, we add some Gaussian noise. The heat kernel is chosen because it simulates a diffusion process. Using de-convolution we aim at recovering the original signal before diffusion. For this experiment, we put ourselves in an ideal case and suppose that both the PSD of the input signal and the noise level are known.

Figure 1 and 2 present the results. We observe that Wiener filtering is able to de-convolve the measurements. The second plot shows the reconstruction errors for three different methods: Tikonov presented in problem, TV and Wiener filtering. Wiener filtering performs clearly much better than the other methods because it has a much better prior assumption.

Signal and filters for a noise level of \(0.16\).

The convolution kernel is \(e^{-\frac{10 x}{\lambda_{\max}}}\).

Evolution of the error with respect of the noise.

Graph de-convolution on a geometric random graph.