GSP_KRON_PYRAMID - compute a pyramid of graphs using the kron reduction
Usage
Gs = gsp_kron_pyramid( G, Nlevels); Gs = gsp_kron_pyramid( G, Nlevels, param);
Input parameters
| G | Graph structure |
| Nlevels | Number of level of decomposition |
| param | Optional structure of parameters |
Output parameters
| Gs | Cell array of graphs |
Description
This function compute a pyramid of graph based on the Kron reduction. The indices are taken as the positive entry of the highest eigenvector.
param is a structure of optional parameters containing the following fields:
lambda: Stability parameter. It add self loop to the graph to give the alorithm some stability (default: 0.025).
sparsify: Sparsify the graph after the Kron reduction (default: 1).
epsilon: Sparsification parameter if the sparsification is used (default: min(2/sqrt(G.N), 0.1) ).
filters: A cell array of filter that will be used for the analysis and sytheis operator. If only one filter is given, it will be used for all levels. You may change that later on. Default
\begin{equation*} h(x) = \frac{0.5}{0.5+x} \end{equation*}
Example:
N = 256;
G = gsp_sensor(N);
Nlevel = 5;
Gs = gsp_kron_pyramid(G, Nlevel);
figure;
for ii = 1:numel(Gs)
subplot(2,3,ii)
gsp_plot_graph(Gs{ii})
title(['Reduction level: ', num2str(ii-1)]);
end
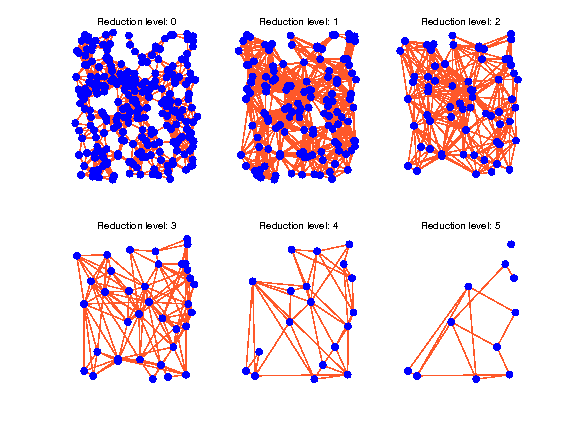
Demo: demo_kron_pyramid
