This is where navigation should be.
GSP_KRON_REDUCE - Performs Kron reduction
Usage
Greduced=gsp_kron_reduce(G,keep_inds); Lreduced=gsp_kron_reduce(L,keep_inds);
Input parameters
| G | Graph structure or graph Laplacian matrix. |
| keep_inds | The set of indices to keep in the reduced graph. |
Output parameters
| Greduced | The Kron-reduced graph structure or Laplacian. |
Description
'gsp_kron_reduce(G,keep_inds)' performs Kron reduction:
\begin{equation*}
{\cal L}_{reduced}={\cal L}_{{\cal V}_1,{\cal V}_1}-{\cal L}_{{\cal V}_1,{\cal V}_2} \left[{\cal L}_{{\cal V}_2,{\cal V}_2}\right]^{-1} {\cal L}_{{\cal V}_2,{\cal V}_1}
\end{equation*}
If a matrix is given, then a matrix is returned
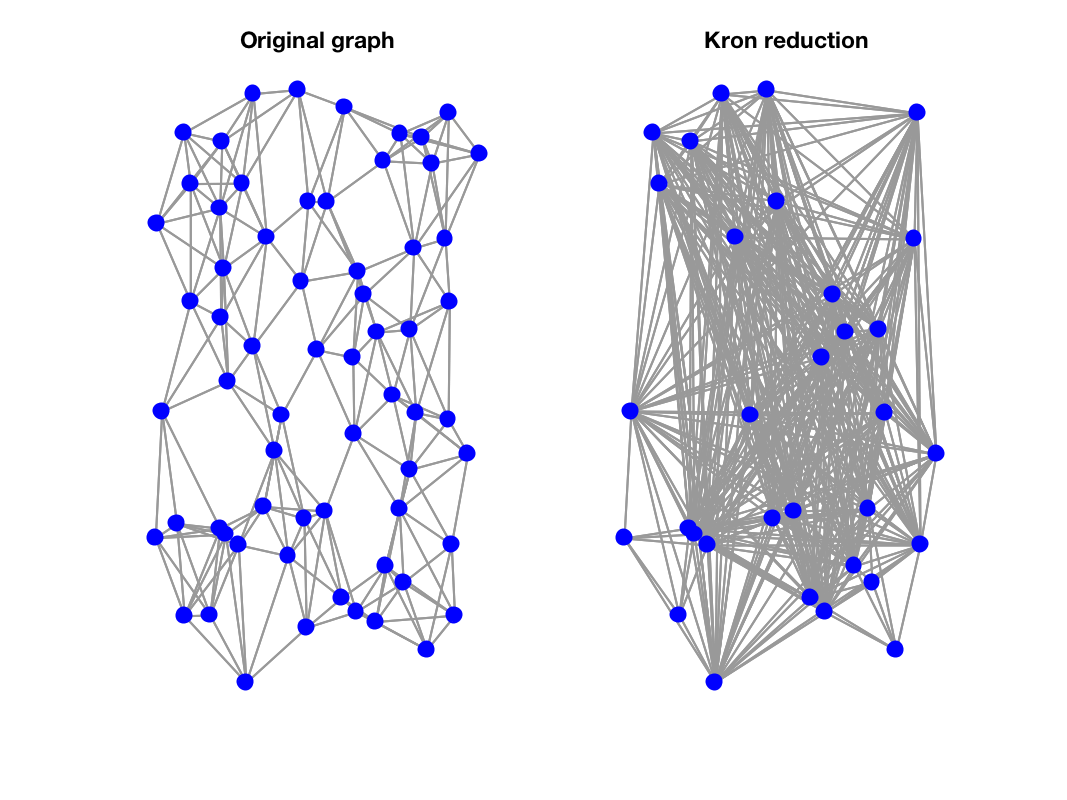
Example:
N = 64;
param.distribute = 1;
param.Nc = 5;
param.regular = 1;
G = gsp_sensor(N,param);
ind = 1:2:N;
Gnew = gsp_kron_reduction( G,ind );
figure;
subplot(121)
gsp_plot_graph(G);
title('Original graph');
subplot(122)
gsp_plot_graph(Gnew);
title('Kron reduction');
Notes: may be able to speed this up with LAMG toolbox
References:
F. Dorfler and F. Bullo. Kron reduction of graphs with applications to electrical networks. Circuits and Systems I: Regular Papers, IEEE Transactions on, 60(1):150--163, 2013.